Die künstliche Intelligenz ChatGPT löst Aufgaben aus dem Mathe-Abi

Mind Blown. Ich kann meinen derzeitigen Zustand nicht anders beschreiben. Eine künstliche Intelligenz löst Mathematikabituraufgaben, obwohl sie dafür niemals trainiert wurde. Aber fangen wir vorne an.

Momentan ist „ChatGPT“ in aller Munde. Das ist eine künstliche Intelligenz, die darauf ausgelegt ist, Fragen zu beantworten. Wenn man so möchte, ein intelligenter Chatbot. Aber fragen wir doch direkt ChatGPT, was es eigentlich ist:

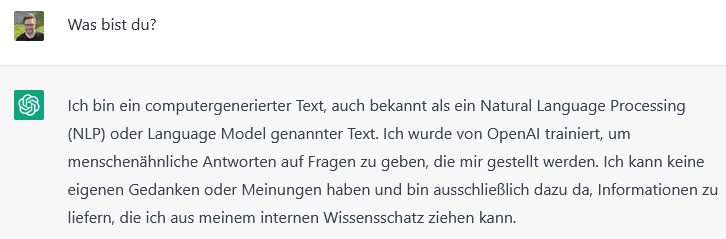
ChatGPT bedient man wie ein Chatprogramm. Man stellt einfach eine Frage und ChatGPT antwortet. In dieser Antwort bezeichnet sich ChatGPT selbst als „computergenerierten Text“. Es meint vermutlich „computergestützter Textgenerator“. Aber es gibt einen Retry-Button, mit dessen Hilfe wir eine neue Antwort generieren können, wenn uns die alte nicht gefällt:

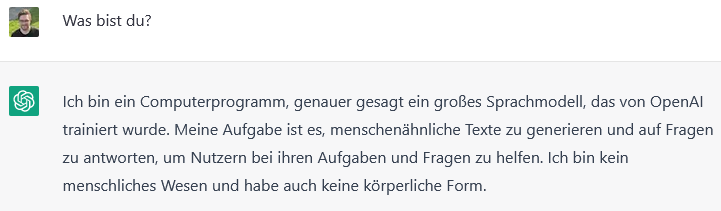
Na das ist doch eine Antwort, mit der ich was anfangen kann! Ich werde an dieser Stelle so ausführlich, weil dadurch etwas deutlich wird: ChatGPT erzeugt authentische Texte. Aber nicht immer beim ersten Versuch und nicht frei von Fehlern. Aber durch Veränderung meiner Eingabe oder einfach Neuberechnung kommen hier erstaunliche Ergebnisse raus. Und ChatGPT macht selbst deutlich klar: Es ist kein Mensch, es kann keine eigenen Gedanken oder Meinungen haben. Es puzzelt nur aus bestehenden Textschnipseln eine möglichst gute Antwort zusammen. Nun stellt sich die Frage, was genau ChatGPT denn so alles puzzeln kann. Also habe ich die KI darum gebeten, Mathematikaufgaben zu lösen und die Antwort hat mich schlichtweg aus den Socken gehauen.

Ich habe ChatGPT eine Aufgabe aus einer Klassenarbeit lösen lassen. Diese lautete wie folgt:

Und ChatGPT antwortete:

Als Mathelehrer steht mein Mund offen. Die KI – die auf diese Aufgabe nie trainiert wurde – weiß, was „Brüche gleichnamig machen“ bedeutet, arbeitet mit den Zahlen aus dem Text, bringt sie auf den kleinsten gemeinsamen Nenner. Sie kommt zu einer schlüssigen und gut begründeten Antwort – zumindest scheinbar. Denn diese Prozesse hat ChatGPT weder durchdacht noch verstanden. Es ist sprachlich ungenau und schreibt „Wenn man die Brüche also durch 15 teilt“, wo aber „Wenn man die Brüche auf den Nenner 15 bringt“ richtig wäre. Dazu muss man nicht dividieren, sondern erweitern! Typischer Fehler. Allerdings macht sie diesen Fehler nur in der verbalen Beschreibung – in der Rechnung stimmt es dann wieder: 1/3 werden mit 5 auf 5/15 erweitert und 2/5 werden mit 3 auf 6/15 erweitert. Probleme hat die KI dann mit 3/4. Wenn wir die mit 3 erweitern, kommen wir auf 9/12, nicht (wie von ChatGPT behauptet) auf 9/15. Bei einem neuen Versuch ist es genau anders herum:

Es gibt also Schwierigkeiten beim Vergleich von drei Brüchen – zwei gehen aber gut! Bitten wir die KI doch mal um einen alternativen Lösungsweg:

Darstellungswechsel in die Dezimalschreibweise – check! Diesmal ein schlüssiges und richtiges Ergebnis beim ersten Versuch. Vielleicht hätte ChatGPT noch darauf eingehen können, dass man für den Vergleich der Zahlen die Stellen von links nach rechts durch geht und die Zehntelstelle hier genauer betrachtet wird – dort ist die 7 größer als die 3 oder die 4. Aber ChatGPT ist wie gesagt keine künstliche Intelligenz, die explizit auf das Lösen von Mathematikaufgaben trainiert wurde.

Und eine „Kleinigkeit“ habe ich bisher verschwiegen. Angeregt durch Sebastian Eisele und Sascha Elsser auf Twitter habe ich die KI nicht nur die Klassenarbeit lösen lassen. Die ganze Klassenarbeit wurde von der KI entwickelt!

Wow. Ich bitte um einen Schwerpunkt auf bildlichen Darstellungen und die Klassenarbeit beginnt mit dem Zeichnen des Zahlenstrahl und forder später die Darstellung des Bruchs 2/4 in einem Rechteck. Aber mehr noch: Die Aufgaben sind vielfältig und bilden verschiedene Tätigkeiten auf verschiedenen Schwierigkeitsgraden ab. Es muss gezeichnet, gerechnet und erklärt werden. Brüche sollen verglichen werden. Fachbegriffe sollen anhand von Beispielen erläutert werden.

Bitte versteht mich an dieser Stelle nicht falsch: Ich würde diese Arbeit so nicht ohne Überarbeitung im Unterricht einsetzen. Aber ich komme nicht darüber hinweg, wie beeindruckend diese von einer künstlichen Intelligenz generierte Klassenarbeit ist.

Aber genug des Vorgeplänkels. Nun wird es ernst: ChatGPT soll Abituraufgaben lösen. Ausgewählt habe ich die Aufgaben von 2016, weil ich die gerade noch hier hatte. Ich musste leider etwas nach einer Aufgabe suchen, die ich ChatGPT präsentieren kann, da viele Aufgaben mit Informationen aus Skizzen arbeiten. Das ist ein Problem, weil die Skizzen nicht in Textform vorliegen und der Chatbot eben nur Text annimmt. Fündig geworden bin ich im hilfsmittelfreien Teil:

HMF 7 – Stochastik
Bei einem Zufallsexperiment wird eine ideale Münze so lange geworfen, bis zum zweiten Mal Zahl (Z) oder zum zweiten Mal Wappen (W) oben liegt.
Als Ergebnismenge wird { ZZ; WW; ZWZ; ZWW; WZZ; WZW } festgelegt.
Begründen Sie, dass dieses Zufallsexperiment kein Laplace-Experiment ist.

Hier eine mögliche Lösungsskizze zu dieser Aufgabe:

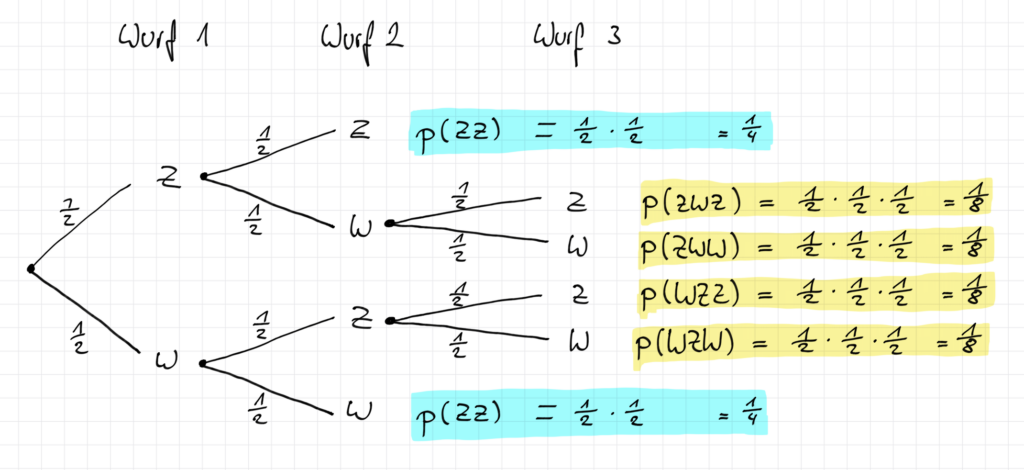
Die kurze Antwort auf die Frage lautet, dass das Zufallsexperiment kein Laplace-Experiment (also ein Experiment bei dem alle Ergebnisse gleichwahrscheinlich sind) ist, da sich zum Beispiel die Wahrscheinlichkeit des Ergebnisses ZWZ mit 1/8 von der Wahrscheinlichkeit des Ergebnisses ZZ mit 1/4 unterscheidet.

Schülerinnen und Schüler müssen zur Beantwortung ein mehrstufiges Zufallsexperiment durchdenken und die Wahrscheinlichkeiten des Münzwurfs (1/2 für Zahl und 1/2 für Wappen) so miteinander verketten. Und die Anzahl der Stufen sind dabei variabel: Landen direkt zweimal Zahl oder zweimal Wappen, bricht das Experiment nach zwei Stufen ab. Sonst ist es ein dreistufiges Experiment. Schülerinnen und Schüler können diese Aufgabe in der Regel gut lösen, wenn sie sich dazu eine Skizze mit Wahrscheinlichkeitsbaum (siehe oben) anlegen. Dennoch sind sie häufig sehr unsicher, da sie von den meisten Zufallsexperimenten gewohnt sind, dass es eine feste Anzahl an Stufen gibt. Wie schlägt sich aber nun die künstliche Intelligenz?

Der erste Versuch geht fatal in die Hose. Wäre das eine Schüler:innen-Lösung hatte man als Lehrkraft beurteilt, dass der oder die Lernende nicht verstanden hat, was ein mehrstufiges Zufallsexperiment ist, da er oder sie sagt, dass die vorgegebene Lösungsmenge nicht zum Experiment passe. Dabei werden noch Münzwurf und Würfeln durcheinander gebracht. Irgendwas mit verschiedenen Kombinationen von Zahl und Wappen scheint aber hängen geblieben zu sein, am Ende wird dann doch irgendwie richtig geraten.

Bei Versuch 4 gehen dann Laplace- und Bernoulli-Experimente durcheinander:

Aber dann kam Versuch 7:

Okay. Not bad und soweit richtig. Aber ich bin skeptisch und hake nach. ChatGPT antwortet beim ersten Versuch:

In dieser Antwort führt die künstliche Intelligenz die Lösung der Aufgabe auf das zugrunde liegende Experiment des Münzwurfs zurück, bestimmt hier die Wahrscheinlichkeiten der Ergebnisse, bildet dann daraus das mehrstufige Zufallsexperiment, berechnet die Wahrscheinlichkeiten von dessen Ergebnissen anhand der Stufen und begründet richtig und logisch schlüssig anhand eines Gegenbeispiels, warum das Experiment kein Laplace-Experiment sein kann.

Spätestens an dieser Stelle kam ich aus dem Staunen nicht mehr heraus. All das passierte völlig ohne zusätzlichen Input von mir. Die KI arbeitet hier ausschließlich mit der Abituraufgabe von 2016 und liefert eine tadellose Lösung ab. Die von mir beschriebenen Gedankengänge zur Lösungsfindung hat ChatGPT so wohl eher nicht durchlaufen. Vermutlich hat sie einfach nur richtig geraten. Eine an schönen Beispielen illustrierte Erläuterung dazu, was ChatGPT nicht kann, findet man drüben bei Armin. Aber so ein präzises richtiges Raten bei Versuch Nummer 7 mit so einer detailreichen Antwort auf Nachfrage ist faszinierend. Und dabei darf man nicht vergessen: Jede dieser sieben Antworten wurde innerhalb von Sekunden generiert. Die KI hat die Lösungen so schnell ausgegeben, wie ich sie lesen konnte.

Fakt ist: Die künstliche Intelligenz ChatGPT ist in der Lage, richtige und gut begründete Lösungen für Mathematikabituraufgaben zu erzeugen. Nicht beim ersten Versuch und auch nicht für alle Aufgaben. Aber wir sollten uns nun die Frage stellen, welche Auswirkungen die Existenz einer solche Technologie auf unsere Prüfungen, unsere Curricula und Schule im Allgemeinen haben sollte.

Wer ChatGPT mal ausprobieren möchte, kann das unter dieser Adresse tun (ein kostenloser Account muss angelegt werden): https://chat.openai.com/